哈夫曼树

基本概念

路径：从树中一个节点到另一个节点之间的分支。
路径长度：路径上的分支数。
树的路径长度：从树根到每一个节点的路径长度之和。

树的带权路径长度

设二叉树具有个 $n$ 带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度（Weighted Path Length of Tree，WPL）。

设 $w_i$ 为二叉树第 $i$ 个叶结点的权值， $l_i$ 为从根结点到第 $i$ 个叶结点的路径长度，则 WPL 计算公式如下：

$$ WPL = \sum_{i=1}^{n} w_i l_i $$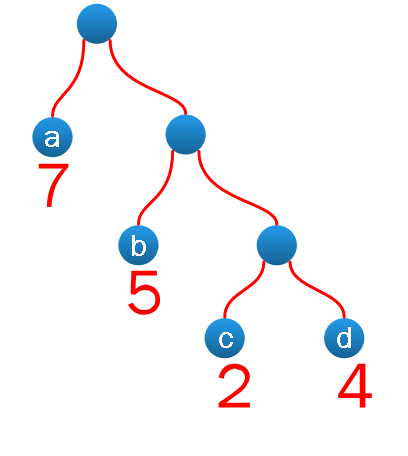

如上图所示，其 WPL 计算过程与结果如下：

$$ WPL=7×1+5×2+2×3+4×3=35 $$

结构

对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，WPL 最小的二叉树 称为 哈夫曼树（Huffman Tree）。

对于哈夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近，此外其仅有叶结点的度为 0，其他结点度均为 2。

哈夫曼算法

哈夫曼算法用于构造一棵哈夫曼树，算法步骤如下：

初始化：由给定的 $n$ 个权值构造 $n$ 棵只有一个根节点的二叉树，得到一个二叉树集合 $F$ 。
选取与合并：从二叉树集合 $F$ 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
删除与加入：从 $F$ 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 $F$ 中。
重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是哈夫曼树。

哈夫曼编码

在进行程序设计时，通常给每一个字符标记一个单独的代码来表示一组字符，即编码。

在进行二进制编码时，假设所有的代码都等长，那么表示 $n$ 个不同的字符需要 $\left \lceil \log_2 n \right \rceil$ 位，称为 等长编码。

如果每个字符的 使用频率相等，那么等长编码无疑是空间效率最高的编码方法，而如果字符出现的频率不同，则可以让频率高的字符采用尽可能短的编码，频率低的字符采用尽可能长的编码，来构造出一种 不等长编码，从而获得更好的空间效率。

在设计不等长编码时，要考虑解码的唯一性，如果一组编码中任一编码都不是其他任何一个编码的前缀，那么称这组编码为 前缀编码，其保证了编码被解码时的唯一性。

哈夫曼树可用于构造 最短的前缀编码，即 哈夫曼编码（Huffman Code）。

证明如下：

设有 $n$ 种字符的电文中每种字符出现的次数为 $w_i$ ，其编码长度为 $l_i$ ，则电文总长为：

$$ \sum_{i=1}^nw_il_i $$

正好是对应的哈夫曼树的WPL。

其构造步骤如下：

设需要编码的字符集为：$d_1,d_2,\dots,d_n$ 他们在字符串中出现的频率为：$w_1,w_2,\dots,w_n$。
以 $d_1,d_2,\dots,d_n$作为叶结点，$w_1,w_2,\dots,w_n$ 作为叶结点的权值，构造一棵哈夫曼树。
规定哈夫曼编码树的左分支代表 0 ，右分支代表 1 ，则从根结点到每个叶结点所经过的路径组成的 0 、1 序列即为该叶结点对应字符的编码。

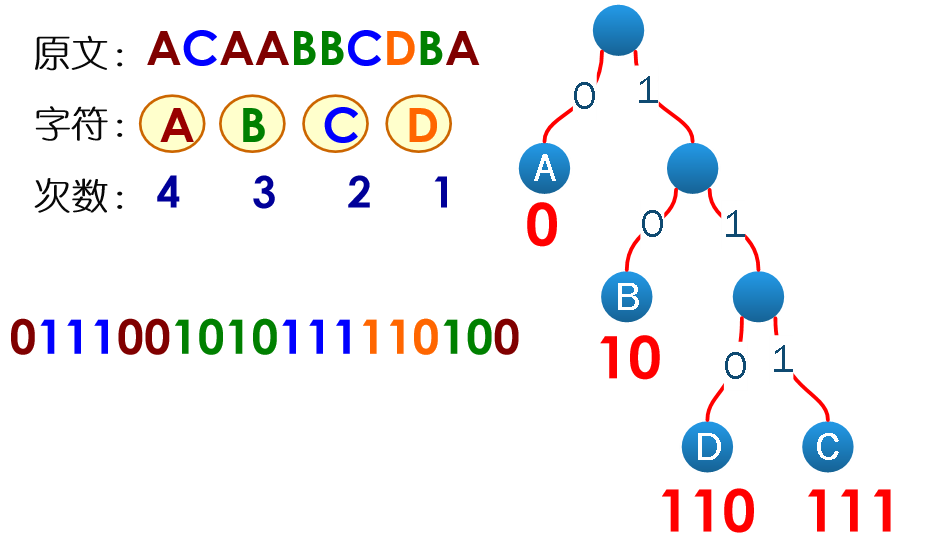
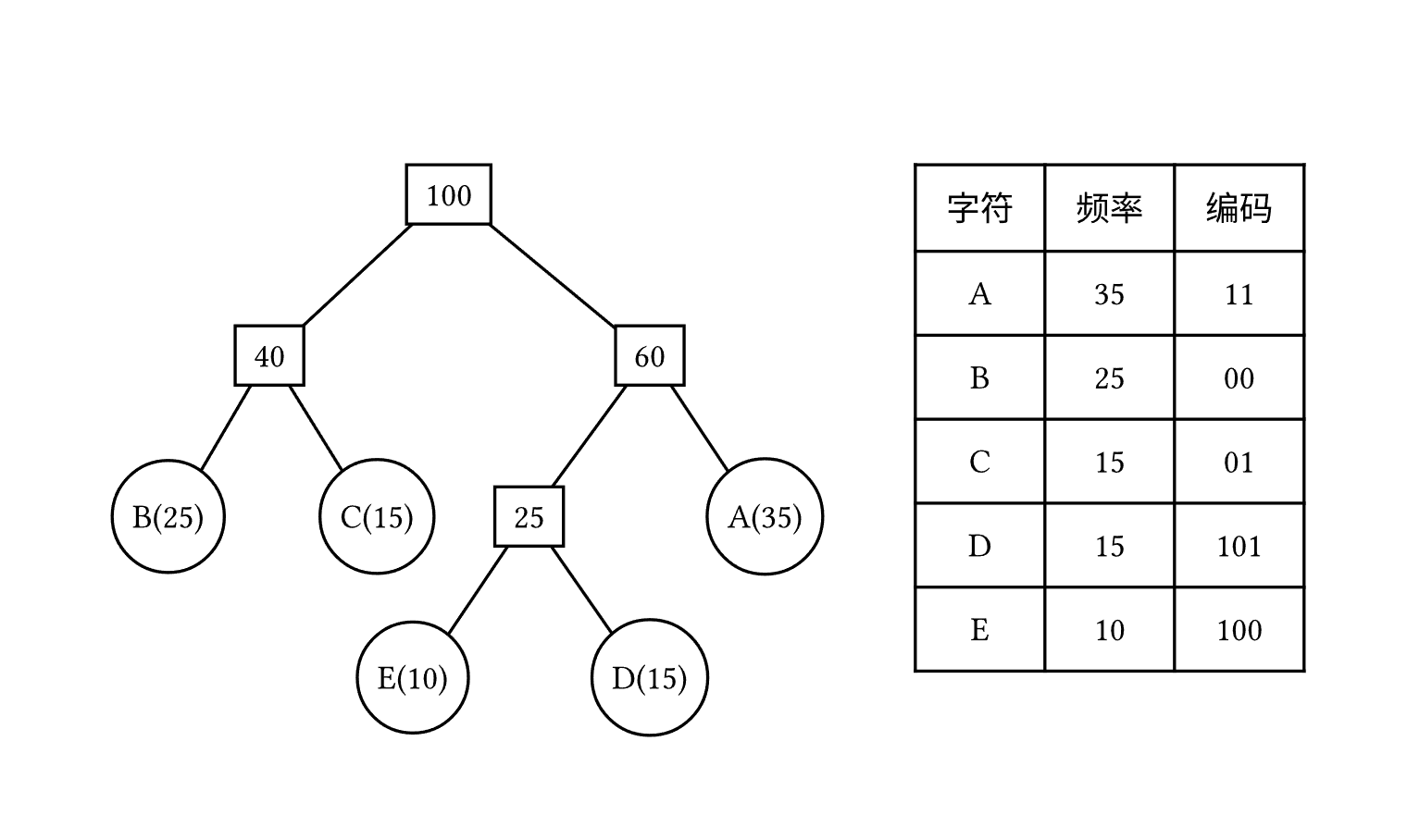
实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58


struct node{
    char name;
    int val;
    node* left;
    node* right;
    node(char c,int a){
        name = c;
        val = a;
        left = right = nullptr;
    }
};

//求WPL
int getWPL(node *root,int dep){
    if(root==nullptr){
        return 0;
    }
    if(root->left == nullptr and root->right == nullptr){
        return root->val * dep;
    }
    return getWPL(root->left,dep + 1) + getWPL(root->right,dep + 1);
}

//求Huffman编码
void buildHuffmanCode(node *root,string s,map<char,string> &mp){
    if(root==nullptr) return;
    if(root->left == nullptr and root->right == nullptr){
        mp[root->name] = s;
    }
    buildHuffmanCode(root->left,s+"0",mp);
    buildHuffmanCode(root->right,s+"1",mp);
}

void solve()
{
    int n;cin >> n; //n<2的情况没有处理，需要自行修改
    priority_queue<node*, vector<node*>, function<bool(node*, node*)>> pq([](node* a, node* b) { return a->val > b->val; });
    for(int i = 0; i < n; i++){
        char c;int t;cin >> c >> t;
        pq.push(new node(c,t));
    }

    // 构建哈夫曼树
    while(pq.size() > 1){
        node* a = pq.top(); pq.pop();
        node* b = pq.top(); pq.pop();
        node* c = new node('$',a->val + b->val);
        c->left = a;
        c->right = b;
        pq.push(c);
    }
    node* root = pq.top();
    cout << getWPL(root,0) << endl;
    map<char,string> mp;
    buildHuffmanCode(root,string(),mp);
    for(auto [c,s] : mp)
        cout << c << " " << s << endl;
}

参考

霍夫曼树 - OI Wiki